Interesante ejemplo sobre el Sistema D´Hondt (fuente: Wikipedia)
Reparto
Tras escrutar todos los votos, se calcula una serie de divisores para cada lista. La fórmula de los divisores es V/N, donde V representa el número total de votos recibidos por la lista, y Nrepresenta cada uno de los números enteros de 1 hasta el número de cargos electos de la circunscripción objeto de escrutinio. Una vez realizadas las divisiones de los votos de cada candidatura por cada uno de los divisores desde 1 hasta N, la asignación de cargos electos se hace ordenando los cocientes de las divisiones de mayor a menor y asignando a cada uno un escaño hasta que éstos se agoten. A diferencia de otros sistemas, el número total de votos no interviene en el cómputo.
[editar]
Ejemplo
Supongamos unas elecciones a las que se presentan cinco partidos, entre los que deben repartirse siete escaños (o curules o bancas, según el país). Como el número total de votos no cuenta, el resultado sería el mismo si concurrieran más partidos con menos de 15.000 votos.
| Partido A | Partido B | Partido C | Partido D | Partido E | |
|---|---|---|---|---|---|
| Votos | 340.000 | 280.000 | 160.000 | 60.000 | 15.000 |
Antes de empezar la asignación de escaños hace falta dibujar una tabla de 7 filas (número de escaños) por 5 columnas (número de partidos). En la primera fila escribimos el número total de votos recibidos por cada partido (divisor 1). Es preferible ordenar los partidos por número de votos, así se simplificarán las siguientes fases del algoritmo.
Primera iteración
- El cociente más alto corresponde al partido A, 340.000 votos.
- El partido A gana un escaño y se escribe debajo el siguiente cociente:
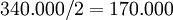. - Se rellena el resto de casillas en blanco con los valores de la casilla inmediatamente superior.
Segunda iteración
- El cociente más alto corresponde al partido B, 280.000 votos.
- El partido B gana un escaño y se escribe debajo el cociente:
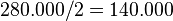. - Rellenamos el resto de casillas en blanco con los valores de la casilla inmediatamente superior.
Tercera iteración
- El cociente más alto corresponde al partido A, 170.000 votos.
- El partido A gana un nuevo escaño y escribimos abajo el siguiente cociente:
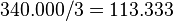. - Rellenamos el resto de casillas en blanco con los valores de la casilla inmediatamente superior.
Cuarta iteración
- El cociente más alto corresponde al partido C, 160.000 votos.
- El partido C gana un escaño y se escribe debajo el siguiente cociente:
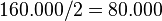. - Rellenamos el resto de casillas en blanco con los valores de la casilla inmediatamente superior.
Quinta iteración
- El cociente más alto corresponde al partido B, 140.000 votos.
- El partido B gana un nuevo escaño y se escribe debajo el siguiente cociente:
. - Rellenamos el resto de casillas en blanco con los valores de la casilla inmediatamente superior.
Sexta iteración
- El cociente más alto corresponde al partido A, 113.333 votos.
- El partido A gana un nuevo escaño y escribimos abajo el siguiente cociente:
. - Rellenamos el resto de casillas en blanco con los valores de la casilla inmediatamente superior.
Séptima iteración
- El cociente más alto corresponde al partido B, 93.333 votos.
- El partido B gana un nuevo escaño y escribiríamos abajo el siguiente cociente:
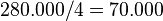, pero como no hay más escaños terminamos aquí. - Rellenamos el resto de casillas en blanco con los valores de la casilla inmediatamente superior.
| Partido A | Partido B | Partido C | Partido D | Partido E | |
|---|---|---|---|---|---|
| Votos | 340.000 | 280.000 | 160.000 | 60.000 | 15.000 |
| Escaño 1 | (340.000/1 =) 340.000 | (280.000/1 =) 280.000 | (160.000/1 =) 160.000 | (60.000/1 =) 60.000 | (15.000/1 =) 15.000 |
| Escaño 2 | (340.000/2 =) 170.000 | (280.000/1 =) 280.000 | (160.000/1 =) 160.000 | (60.000/1 =) 60.000 | (15.000/1 =) 15.000 |
| Escaño 3 | (340.000/2 =) 170.000 | (280.000/2 =) 140.000 | (160.000/1 =) 160.000 | (60.000/1 =) 60.000 | (15.000/1 =) 15.000 |
| Escaño 4 | (340.000/3 =) 113.333 | (280.000/2 =) 140.000 | (160.000/1 =) 160.000 | (60.000/1 =) 60.000 | (15.000/1 =) 15.000 |
| Escaño 5 | (340.000/3 =) 113.333 | (280.000/2 =) 140.000 | (160.000/2 =) 80.000 | (60.000/1 =) 60.000 | (15.000/1 =) 15.000 |
| Escaño 6 | (340.000/3 =) 113.333 | (280.000/3 =) 93.333 | (160.000/2 =) 80.000 | (60.000/1 =) 60.000 | (15.000/1 =) 15.000 |
| Escaño 7 | (340.000/4 =) 85.000 | (280.000/3 =) 93.333 | (160.000/2 =) 80.000 | (60.000/1 =) 60.000 | (15.000/1 =) 15.000 |
| Total de cargos electos | 3 | 3 | 1 | 0 | 0 |
| % votos | 40% | 33% | 19% | 7% | 2% |
| % escaños | 43% | 43% | 14% | 0% | 0% |
En la siguiente tabla se muestra el mismo procedimiento, pero en lugar de calcular los cocientes conforme se van asignando los escaños se han calculado todos en primer lugar.
- Cada fila corresponde a uno de los partidos.
- Cada columna corresponde a un divisor.
- El número entre corchetes ([]) indica el número de orden en la secuencia.
- Las celdas verdes son aquellas a las que se ha asignado un escaño.
| Divisor | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Partidos | A | [1] 340.000 | [3] 170.000 | [6] 113.333 | 85.000 | 68.000 | 56.667 | 48.571 |
| B | [2] 280.000 | [5] 140.000 | [7] 93.333 | 70.000 | 56.000 | 46.667 | 40.000 | |
| C | [4] 160.000 | 80.000 | 53.333 | 40.000 | 32.000 | 26.667 | 22.857 | |
| D | 60.000 | 30.000 | 20.000 | 15.000 | 12.000 | 10.000 | 8.571 | |
| E | 15.000 | 7.500 | 5.000 | 3.750 | 3.000 | 2.500 | 2.143 | |
[editar]
Ejemplo 2
En este ejemplo, utilizado en la Facultad de Economía y Empresa de la Universidad de Zaragoza para la asignatura Política Económica, se usan los mismos datos ficticios que los usados en los ejemplos del Método del resto mayor, para permitir comparaciones.
Suponiendo que se presenten siete partidos para elegir 21 escaños, los partidos reciben 1.000.000 votos repartidos así:
| Partido A | 391.000 votos |
| Partido B | 311.000 votos |
| Partido C | 184.000 votos |
| Partido D | 73.000 votos |
| Partido E | 27.000 votos |
| Partido F | 12.000 votos |
| Partido G | 2.000 votos |
- Cada fila corresponde a uno de los partidos.
- Cada columna corresponde a un divisor.
- El número entre corchetes ([]) indica el número de orden en la secuencia.
- Las celdas verdes son aquellas a las que se ha asignado un escaño.
| Divisor | Reparto | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Total | % Escaños | ||
| Partidos | A | [1] 391.000 | [3] 195.500 | [6] 130.333 | [8] 97.750 | [10] 78.200 | [13] 65.166 | [16] 55.857 | [18] 48.875 | [21] 43.444 | 39.100 | 9 | 42,86% |
| B | [2] 311.000 | [5] 155.500 | [7] 103.666 | [11] 77.750 | [14] 62.200 | [17] 51.833 | [20] 44.428 | 38.875 | 34.555 | 31.100 | 7 | 33,33% | |
| C | [4] 184.000 | [9] 92.000 | [15] 61.333 | [19] 46.000 | 36.800 | 30.666 | 26.285 | 23.000 | 20.444 | 18.400 | 4 | 19,05% | |
| D | [12] 73.000 | 36.500 | 24.333 | 18.250 | 14.600 | 12.166 | 10.428 | 9.125 | 8.111 | 7.300 | 1 | 4,76% | |
| E | 27.000 | 13.500 | 9.000 | 6.750 | 5.400 | 4.500 | 3.857 | 3.375 | 3.000 | 2.700 | 0 | 0.00% | |
| F | 12.000 | 6.000 | 4.000 | 3.000 | 2.400 | 2.000 | 1.714 | 1.500 | 1.333 | 1.200 | 0 | 0.00% | |
| G | 2.000 | 1.000 | 666 | 500 | 400 | 333 | 285 | 250 | 222 | 200 | 0 | 0.00% | |
Los 21 escaños quedan repartidos así:
| Partido A | 9 escaños |
| Partido B | 7 escaños |
| Partido C | 4 escaños |
| Partido D | 1 escaño |
| Partido E | 0 escaños |
| Partido F | 0 escaños |
| Partido G | 0 escaños |
[editar]
Influencia de las leyes electorales en los resultados
A veces, las leyes electorales fijan un porcentaje mínimo de votos, tal que los partidos que no consigan alcanzar ese umbral o barrera electoral quedan excluidos del cuerpo deliberante. A este porcentaje se le suele denominar porcentaje de exclusión y no es parte del sistema D'Hondt. Dependiendo de la ley electoral el porcentaje de votos puede ser calculado sobre el conjunto total de votos o sobre el conjunto de votos válidos (quitando nulos).
El porcentaje de exclusión se puede establecer a nivel de circunscripción (ámbito donde se aplica el sistema D'Hondt), a nivel del conjunto de todas las circunscripciones o alguna combinación de ambas. Ejemplos en España:
- Elecciones al Congreso de los Diputados - Elecciones autonómicas de Cataluña, Aragón y Andalucía :
- Circunscripciones:Las provincias
- Porcentaje de exclusión: Se aplica a nivel de circunscripción y es del 3%
- Circunscripciones: Circunscripción única (el conjunto total)
- Porcentaje de exclusión: 5%
- Las elecciones autonómicas de Castilla y León también usan un porcentaje de exclusión del 5% pero aplicado a las circunscripciones que son las provincias.
- Circunscripciones: 5 (cada circunscripción está formada por uno o más municipios)
- Porcentaje de exclusión: Se aplica a nivel del conjunto de circunscripciones y es del 5%
- Las elecciones autonómicas de la Comunidad Valenciana son similares a estas pero usando como circunscripciones las provincias y usando el porcentaje de exclusión sobre el total de votos emitidos (incluye nulos) en lugar de los votos válidos.
- Circunscripciones: Las islas
- Porcentaje de exclusión: Para poder obtener escaño hay que tener un 6% a nivel de comunidad o bien ganar o tener un 30% en alguna de las circunscripciones.
El orden en que se repartan los cargos electos a los individuos de cada lista podría no estar dado por este sistema: puede ser una decisión interna del partido (en un sistema de listas cerradas) o puede que los votantes ejerzan alguna influencia (en un sistema de listas abiertas).
Para el número de cargos electos en una circunscripción electoral única, este sistema se comporta como un sistema proporcional puro. Si se fragmenta su aplicación por circunscripciones, suele sufrir una distorsión y los resultados totales pueden no ser proporcionales al número de votos válidos.
No hay comentarios:
Publicar un comentario